
Let's sort it out!
In a series of posts, we will be discussing some of the sorting algorithms listed in the below order:
Selection Sort
Quick Sort
Heap Sort
In this post, we will explore the next, in a series of sorting algorithms, the selection sort. If you feel nostalgic about sorting algorithms, I don’t blame you and it’s totally fine if you want to skim through the first post of the series on Bubble Sort. Good read eh! Now you know that bubble sort’s time and space complexity is kind of meh! We crave for a faster and more efficient algorithm to sort the long list of input elements. Is “Selection Sort” the answer? Maybe.
Why is it called Selection Sort?
The sorting algorithm gets its name from the iterations it performs through input arrays or elements. The algorithm selects the current smallest element and swaps it into its sorted place and continues doing it until the list is sorted. It creates two sections of the arrays; one section is unsorted, and another is sorted. In short, we will be selecting one item at a time by its size and moving it to its sorted position.
Breaking down the instructions:
Given an unsorted array, set the first index [0] element as the smallest number.
Iterate through the array to find the smallest number.
Now swap the smallest number as Index [0] and the original index [0] value to index of the smallest number.
Continue the above process for the rest of the unsorted array until the last element is reached.
I know, it’s like “yeah I get it, but wait I’m lost” and that’s why we have visuals! Yay!
We will pick up the same numbers we introduced during the bubble sort as an example. Yes! I’m trying to make you compare the techniques already.
Let’s play with the selections:
Problem: Sort the numbers [10, 4, 8, 6, 1]. Let’s start with the first iteration of the unsorted list based on our understanding of the above instruction.
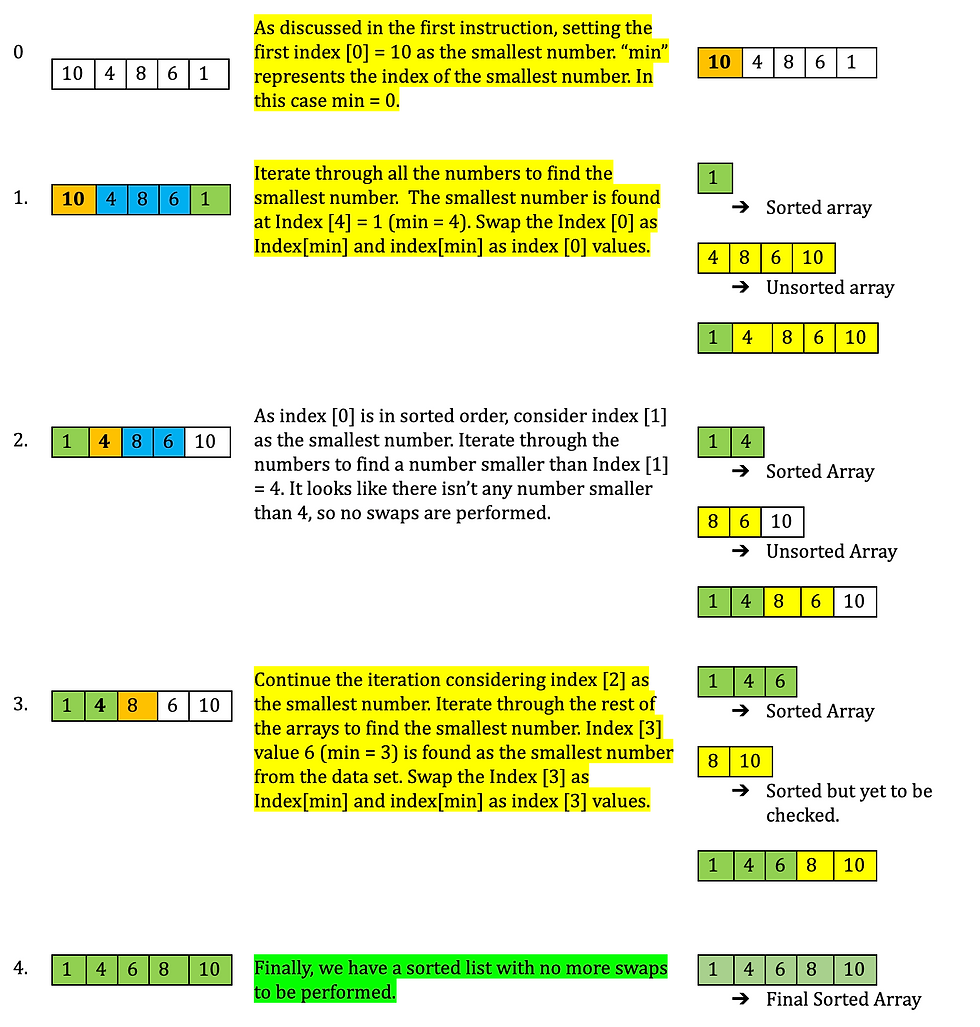
Observations based on Iterations:
In our example, the array size is n=5 and 4 iterations were performed. Similarly, for ‘n’ numbers ‘n-1’ iterations will be performed.
Only one element gets sorted on each pass.
The number of comparisons needed for first iterations was (n-1), as we compared 4 elements to find the smallest number. Likewise, comparisons needed for the second iteration is (n-2), third is (n-3), and so on.
The total number of comparisons required to sort n=5 elements are (n-1) +(n-2) +(n-3) +(n-4). From our example problem length of array is n= 5, no. of comparisons is 4+3+2+1 = 10.
Summation of the above stated turns out to be ‘n(n-1)/2’. So, guess what would be the total # of comparisons if n=100.
In the case of a sorted list, selection sort requires the same number of steps as running through an unsorted list.
The default implementation of selection sort is not stable; however, it can be made stable if required. To explore more about stable selection sort, refer to this link.
Selection Vs Bubble Sort
In bubble sort, the adjacent element is compared and swapped, whereas in selection sort the smallest element is selected to swap against the largest element.
The selection sort has improved efficiency and is faster when compared to bubble sort.
The number of swaps is O(n) in comparison to О(n^2) of bubble sort. In our example , we have very few swaps when compared to swaps in bubble sort.
The worst-case complexity in both algorithms is О(n^2). In the case of an unsorted list, selection sort has to iterate over each of the ‘n’ elements to find the smallest number. One has to repeat ‘n’ times to sort out the array.
In the best case of an already sorted list, selection sort will need to iterate over all elements to check if it's sorted. Due to this reason, the time complexity remains the same as in the worst case О(n^2).
The best case of bubble sort is O(n) because in the first iteration, if the swaps are zero the array is determined to be completely sorted.
Bubble sort consumes additional space for storing variables and needs more swaps, whereas selection sort is an in-place algorithm, so it doesn’t need to allocate any memory.
Selection sort stores one minimum value and its index to compare results. The space required doesn’t increase with the input size, hence space complexity remains O(1).
Time and space complexity are listed in the below table:

Code Implementation:
Note: The code has a couple of counters and log messages only for demonstration purposes.
Log Output:
Let’s decipher the log output to align with our understanding of selection sort.
If you analyze the short unsorted list [10,4,8,6,1] log, length of the array is 5, total iterations performed are 4 and total Comparisons 10. The total comparison value is based on our earlier formulae n(n-1) /2.
Another test performed with a long unsorted list has log output of array length as n=13, total iterations performed (n-1) = 12, total comparisons as 78 based on the above formulae. If you recollect, we had to guess what would be the total comparisons for n=100, it will be 4950.
We also tested a completely sorted array [1,2,3,4,5], although no swapping was required, the total number of comparisons remains 10 and iterations as 4. This clearly justifies the selection sort time complexity of О(n^2) in best and worst cases.
Final thoughts
Selection sort is yet another simple algorithm that is slow and not fast in comparison to bubble sort. However, it works well with a small list to be sorted and in cases where space is limited. This feature is attributed mainly due to the minimal swaps O(n) requiring very less space.
To conclude, selection sort doesn’t seem to be the answer for the fast and efficient sorting algorithm we were looking for at the beginning of the post. However, this isn’t the end of it, in the continuum we have a couple more sorting algorithms to be discussed, to arrive at the most efficient sorting techniques.
Stay tuned!!
I hope you enjoyed the post. Please subscribe to ProstDev for more exciting topics.
Hasta luego, amigos!
Study Resources
Below are some resources which discuss Selection sort and its Time-Space complexity at length.
I loved the comparison with the Bubble Sort. That helped me picture it better!